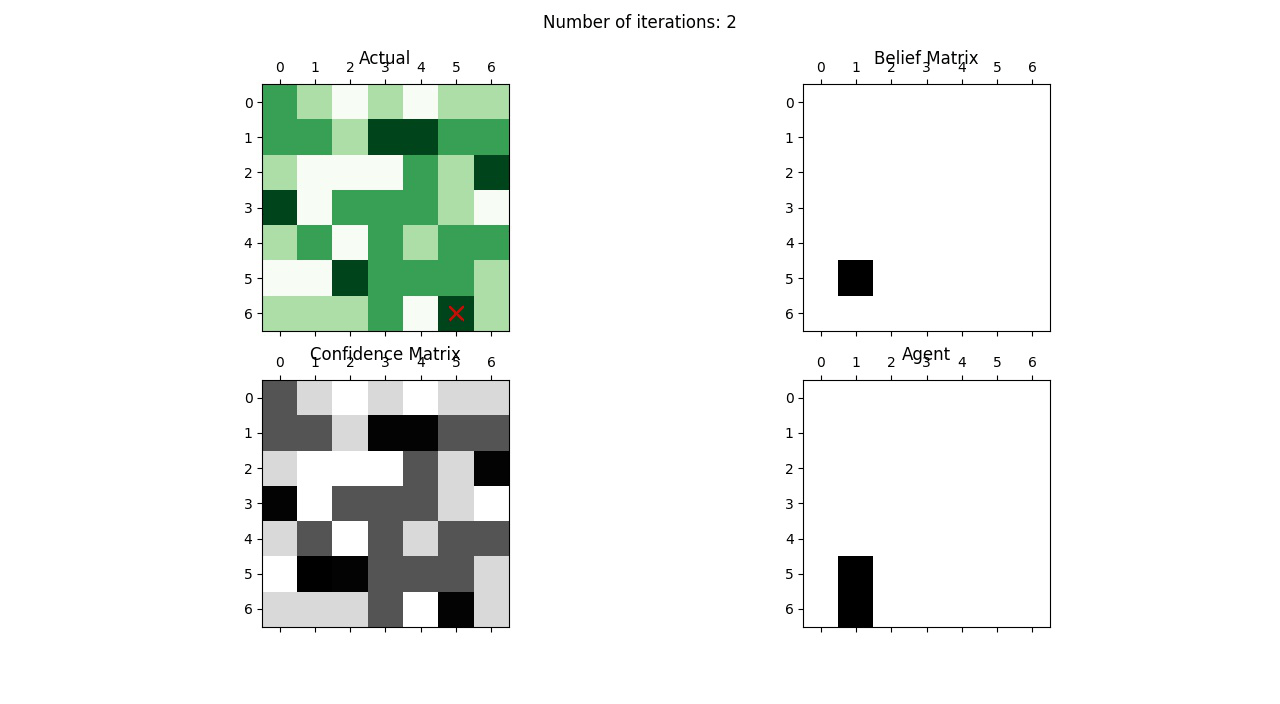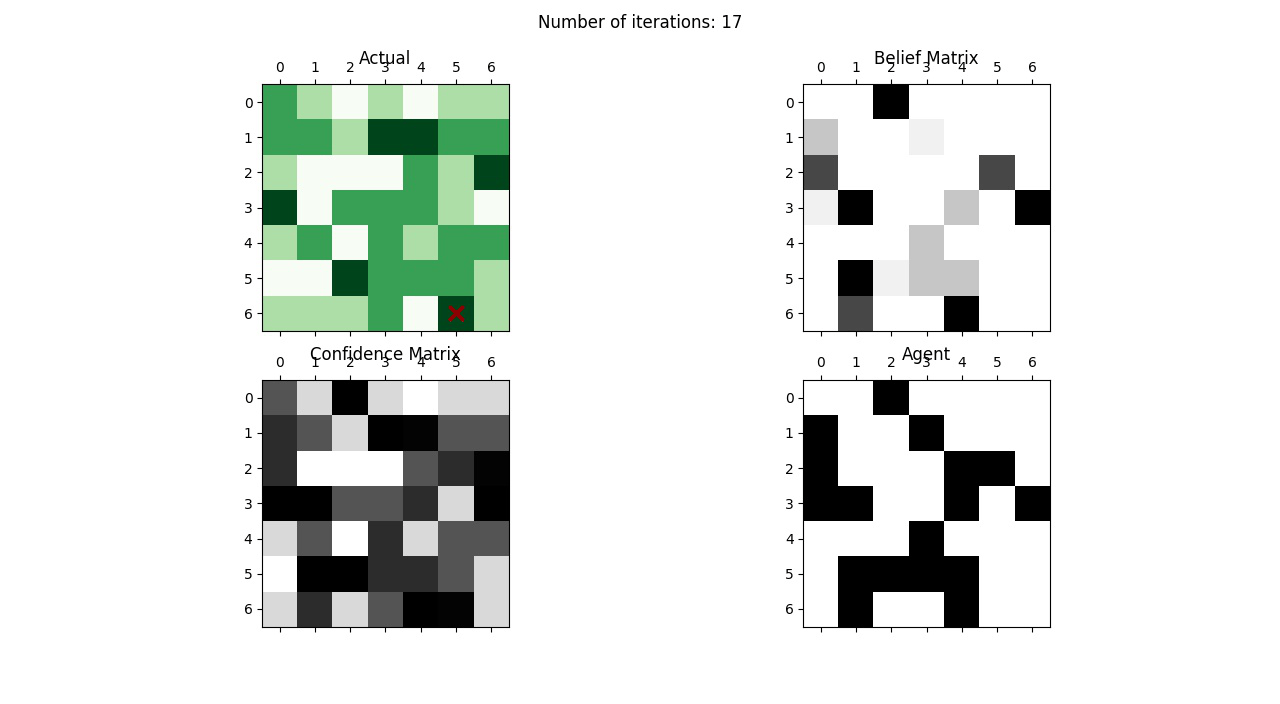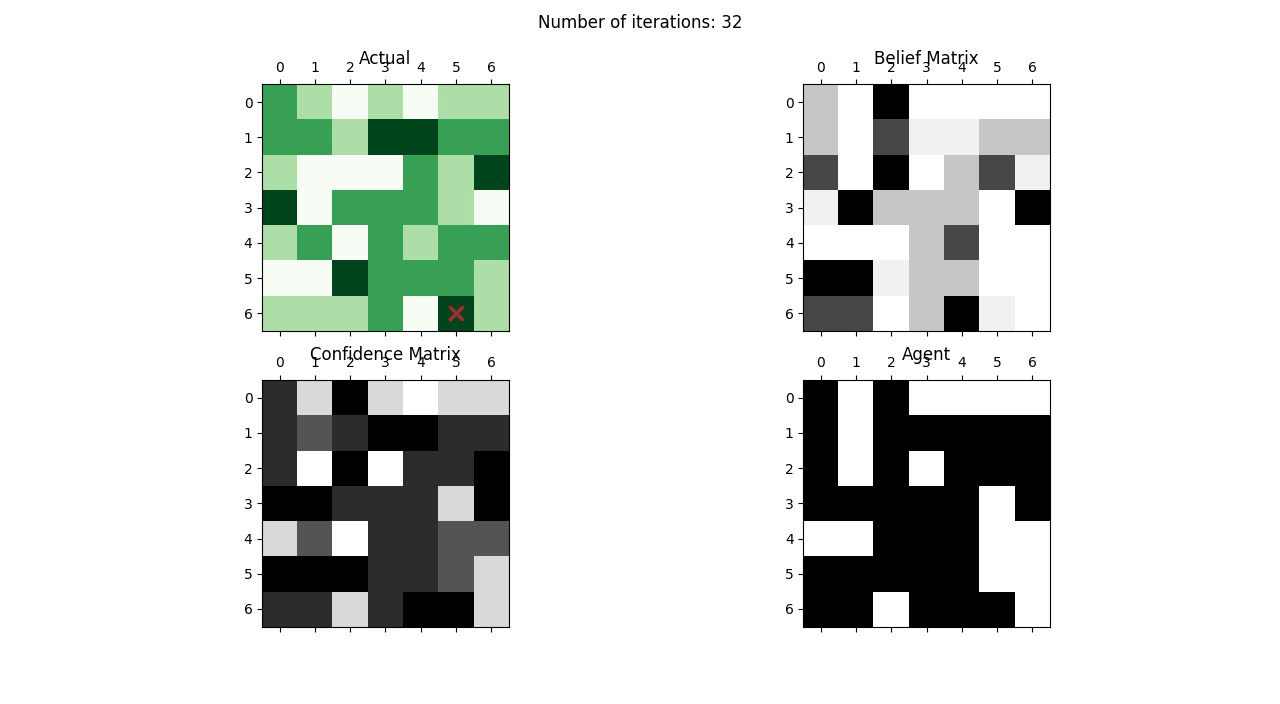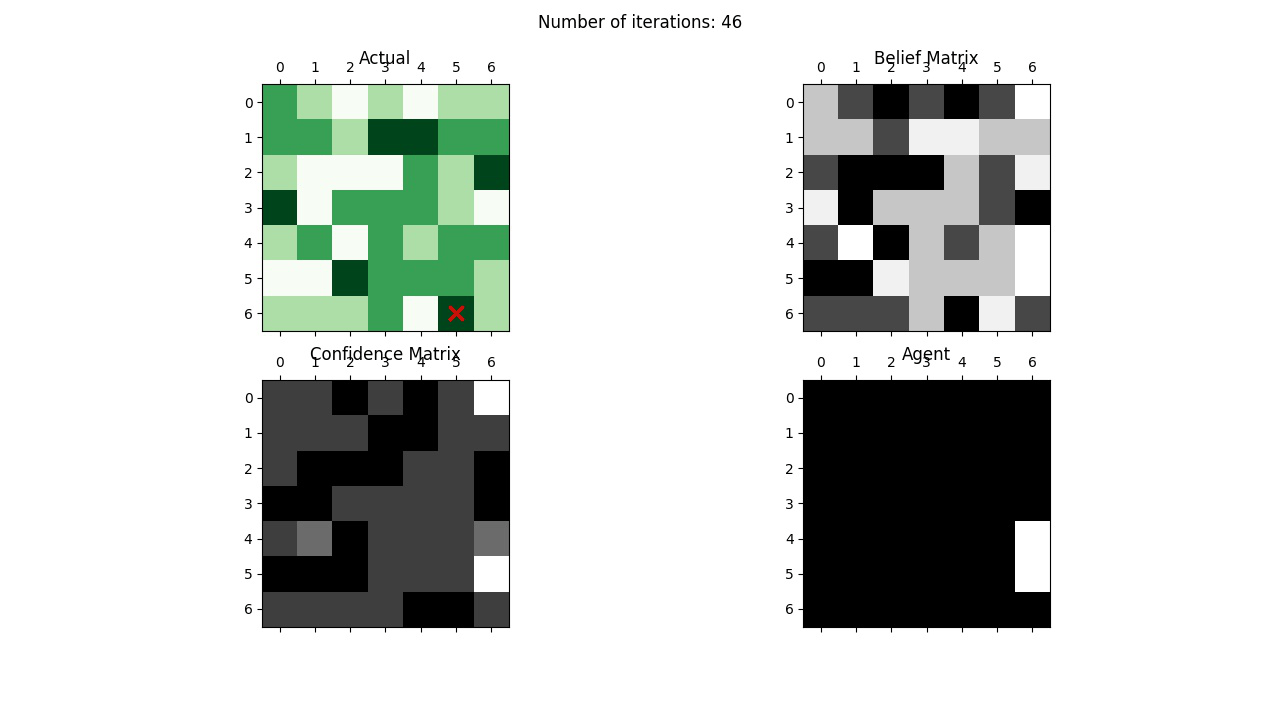
Probablistic Search and Destroy
The problem is this: Given a simulated environment with four different terrains - flat, hilly, forest, a complex maze of tunnels and caves - and a target hiding in this environment, we need to detect the location of the target by updating our prior beliefs. Initially, the target is equally likely to be in any of the cells/terrains and this is our initial prior belief. We then start increasing our beliefs based on the following conditions:
P ( Target not found in Cell | Target is in Cell ) = 0.1, if Cell is flat
P ( Target not found in Cell | Target is in Cell ) = 0.3, if Cell is Hilly
P ( Target not found in Cell | Target is in Cell ) = 0.7, if Cell is Forest
P ( Target not found in Cell | Target is in Cell ) = 0.9, if Cell is a Maze of Caves
I used Bayesian Networks to model this information and update the beliefs of the agent. Being a search problem, the agent uses two rules to find the target:
Rule 1: At any time, search the cell with the highest probability of containing the target.
Rule 2: At any time, search the cell with the highest probability of finding the target.
Using these rules the confidence of the agent is updated and its beliefs become stronger. The following image shows the updation of beliefs as the agent searches for the target in the environment.